Page 18 - XXIII_Studencka_Sesja_Plakatowa
P. 18
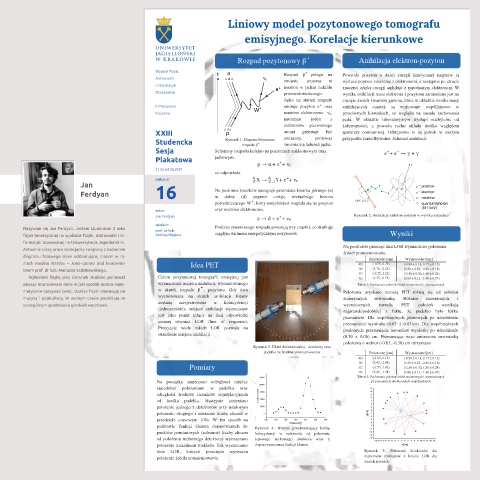
Liniowy model pozytonowego tomografu
emisyjnego. Korelacje kierunkowe
Rozpad pozytonowy β + Anihilacja elektron-pozyton
Wydział Fizyki, +
Rozpad β polega na Powstały pozyton o dużej energii kinetycznej najpierw ją
Astronomii
zmianie protonu w wytraca poprzez zderzenia z elektronami, a następnie po utracie
i Informatyki neutron w jądrze nuklidu znacznej części energii anihiluje z napotkanym elektronem. W
Stosowanej wyniku anihilacji masa elektronu i pozytonu zamieniana jest na
promieniotwórczego.
Jądro na skutek rozpadu energie dwóch kwantów gamma, które w układzie środka masy
+
II Pracownia emituje pozyton e oraz anihilujących cząstek są emitowane współliniowo w
jeden z pędu. W układzie laboratoryjnym wystąpi odchylenie od
Fizyczna neutrino elektronowe ν , przeciwnych kierunkach, ze względu na zasadę zachowania
e
natomiast
elektronów pierwotnego
kolinearności, z powodu ruchu układu środka względem
XXIII atomu przestaje być aparatury pomiarowej. Odstępstwa te są jednak w naszym
Studencka Rysunek 1: Diagram Feynmana związany, ponieważ przypadku zaniedbywalne. Schemat anihilacji:
+
zmienia sią ładunek jądra.
rozpadu β
Sesja Schematy rozpadu kolejno na poziomach nukleonowym oraz e + e → γ + γ
_
+
Plakatowa jadrowym: +
p → n + e + ν e
31.05-04.06.2021
co odpowiada
A
A
+
plakat nr Z X → Y+ e + ν e
Z -1
Jan
Ferdyan 16 Na poziomie kwarków następuje przemiana kwarku górnego (u)
emisję
poprzez
dolny
w
(d)
wirtualnego
bozonu
+
pośredniczącego W , który natychmiast rozpada się na pozyton
autor: oraz neutrino elektronowe. +
Jan Ferdyan + Rysunek 2: Anihilacja elektron-pozyton w wyniku rozpadu β
u → d + e + ν e
opiekun:
Nazywam się Jan Ferdyan. Jestem studentem 3 roku prof. dr hab. Podczas omawianego rozpadu powstają trzy cząstki, co skutkuje
fizyki teoretycznej na wydziale Fizyki, Astronomii i In- Andrzej Magiera ciągłym widmem energetycznym pozytonów. Wyniki
formatyki Stosowanej na Uniwersytecie Jagiellońskim.
Jan Ferdyan Na podstawie przecięć linii LOR wyznaczono połozenia
Aktualnie piszę pracę licencjacką związaną z badaniem
Nazywam się Jan Ferdyan. Jestem studentem 3 roku fizyki teoretycznej na wydziale źródeł promieniowania.
diagramu fazowego silnie oddziałującej materii w ra-
Fizyki, Astronomii i Informatyki Stosowanej na Uniwersytecie Jagiellońskim. Zmierzone [cm] Wyznaczone [cm]
Aktualnie piszę pracę licencjacką związaną z badaniem diagramu fazowego silnie
mach modelu Nambu – Jona-Lasinio pod kierownic-
oddziałującej materii w ramach modelu Nambu - Jona-Lasinio pod kierownictwem Idea PET 4D (-0.75, 0.75) (-0.99 ± 0.11, 0.15 ± 0.12)
prof. dr hab. Mariusza Sadzikowskiego. 7F (3.75, -2.25) (3.39 ± 0.23, -2.82 ± 0.18)
twem prof. dr hab. Mariusza Sadzikowskiego.
Wybrałem fizykę jako kierunek studiów, ponieważ zawsze interesowało mnie w jaki 3C (-2.25, 2.25) (-2.56 ± 0.30, 1.56 ± 0.24)
Wybrałem fizykę jako kierunek studiów, ponieważ
sposób można matematycznie opisywać świat. Oprócz fizyki interesuję się muzyką i Celem pozytonowej tomografii emisyjnej jest 7E (3.75, -0.75) (3.80 ± 0.11, -1.40 ± 0.07)
popkulturą. W wolnym czasie podróżuję ze szczególnym upodobania górskich
wędrówek. zawsze interesowało mnie w jaki sposób można mate- wyznaczenie miejsca anihilacji, wyemitowanego Tabela 1: Porównanie położeń źródeł zmierzonych i wyznaczonych
+
matycznie opisywać świat. Oprócz fizyki interesuję się w skutek rozpadu β , pozytonu. Gdy dwa Położenia uzyskane metodą PET różnią się od położeń
wyemitowane na skutek anihilacji fotony
muzyką i popkulturą. W wolnym czasie podróżuję ze zmierzonych suwmiarką. Różnice zmierzonych i
zostaną zarejestrowane w koincydencji
szczególnym upodobania górskich wędrówek. wyznaczonych metodą PET położeń wynikają
(jednocześnie), miejsce anihilacji wyznaczane najprawdopodobniej z faktu, że pudełko było lekko
jest jako punkt leżący na linii odpowiedzi przesuniete. Dla współrzędnych pionowych po uśrednieniu
zwanej również LOR (line of response). przesunięcie wyniosło (0.63 ± 0.05)cm. Dla współrzędnych
Przecięcie wielu takich LOR pozwala na poziomych przesunięcię natomiast wyniosło po uśrednieniu
określenie miejsca anihilacji.
(0.30 ± 0.06) cm. Przesuwając więc zmierzone suwmiarką
położenia o wektor (-0.63, -0.30) cm otrzymano
Rysunek 3: Układ doświadczalny - detektory oraz
pudełko ze źródłem promieniowania Zmierzone [cm] Wyznaczone [cm]
4D (-1.05, 0.12) (-0.99 ± 0.11, 0.15 ± 0.12)
7F (3.45, -2.88) (3.39 ± 0.23, -2.82 ± 0.18)
Pomiary 3C (-2.55, 1.62) (-2.56 ± 0.30, 1.56 ± 0.24)
7E (3.45, -1.38) (3.80 ± 0.11, -1.40 ± 0.07)
Tabela 2: Porównanie położeń źródeł zmierzonych i wyznaczonych
Na początku zmierzono odległości między po przesunięciu środka układu współrzędnych
sąsiednimi położeniami w pudełku oraz
odległości środków liczników scyntylacyjnych
od środka pudełka. Następnie zmieniano
położenie jednego z detektorów przy ustalonym
położeniu drugiego i mierzono liczbę zliczeń w
przedziale czasowym 100s. W ten sposób na
podstawie funkcji Gaussa dopasowanych do Rysunek 4: Wykres przedstawiający liczbę
punktów pomiarowych (zależność liczby zliczen koincydencji w zależności od położenia
od położenia ruchomego detektora) wyznaczano kątowego ruchomego detektora wraz z
położenie maksimum rozkładu. Tak wyznaczano dopasowaną sumą funkcji Gaussa
linie LOR, których przecięcie wyznacza Rysunek 5: Położenia detektorów dla
położenie źródła promieniowania. maksimów rozkładów z liniami LOR dla
dwóch źródełek