Page 19 - XXIII_Studencka_Sesja_Plakatowa

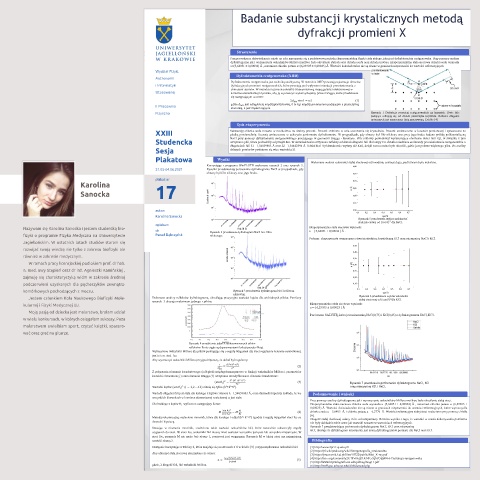
Badanie substancji krystalicznych metodą

dyfrakcji promieni X

Streszczenie

Przeprowadzone doświadczenie miało na celu zapoznanie się z podstawową metodą eksperymentalną fizyki ciała stałego, jaką jest dyfraktometria rentgenowska. Przy pomocy analizy

dyfraktogramu jak i wyznaczeniu wskaźników Millera możliwe było określenie stałych sieci chlorku sodu oraz chlorku potasu. Eksperymentalna stała sieciowa chlorku sodu wyniosła
a=(5,64051 ± 0,00034) Å , natomiast chlorku potasu a=(6,29305 ± 0,00023) Å. Wartości doświadczalne nie są równe w granicach niepewności do wartości referencyjnych

Wydział Fizyki,
Dyfraktometria rentgenowska (XRD)
Astronomii

Dyfraktometria rentgenowska jest techniką analityczną. W metodzie XRD powstają rejestracje obrazów
i Informatyki dyfrakcyjnych promieni rentgenowskich, które powstają pod wpływem interakcji promieniowania z
chmurami atomów. W metodzie tej można określić trójwymiarową mapę gęstości elektronowej w
Stosowanej komórce elementarnej kryształu, aby ją wyznaczyć wykorzystujemy prawo Bragga, które przedstawia

się następującym wzorem:

2 ℎ sin = (1)

II Pracownia gdzie ℎ jest odległością międzypłaszyznową, θ to kąt między promieniem padającym a płaszczyzną
atomową, n jest rządem ugięcia.

Fizyczna Rysunek 1 Dyfrakcja promieni rentgenowskich na krysztale. Dwie fale
padające odbijają się od dwóch płaszczyzn kryształu. Różnica długości
optycznych jest zaznaczona linią przerywaną. Źródło: [4]

Opis eksperymentu

XXIII Substancję chlorku sodu roztarto w moździerzu na drobny proszek. Proszek zrobiono w celu utworzenia się krystalitów. Proszek umieszczono w kuwecie pomiarowej i sprasowano na

gładką powierzchnię. Kuwetę umieszczono w uchwycie goniometru dyfraktometru. W przypadkach, gdy obecny był filtr niklowy oraz przy jego braku badano próbkę polikrystaliczną

Studencka NaCl przy pomocy dyfraktometru rentgenowskiego pracującego w geometrii Bragga - Brentano. Filtr niklowy powodował wystarczające obniżenie ilości linii Kβ, w związku z tym
otrzymano piki, które pochodziły od przejść Kα. W doświadczeniu otrzymano refleksy od dwóch długości fali dla lampy Cu. Źródła miedziane emitowały promieniowanie rentgenowskie o

długościach fali λ1= 1,54059803 Å oraz λ2= 1,54442596 Å. Udział Kα1 był dwukrotnie wyższy niż Kα2, dzięki temu można było określić, gdzie jest połowa większego piku. Do analizy
Sesja dalszych pomiarów posłużono się więc wartością λ1.

Plakatowa Wyniki Wykonano wykres zależności stałej sieciowej od kwadratu cosinusa kąta, pod którym były maksima.

Korzystając z programu WinPLOTR wykonano rysunek 2 oraz rysunek 3. 5,80

31.05-04.06.2021 Rysunki przedstawiają porównanie dyfraktogramu NaCl w przypadkach, gdy
obecny był filtr niklowy oraz jego braku. 5,75

plakat nr 5,70
Karolina 10 4 a [Å] 5,65

Sanocka 17 Liczba zliczeń 10 3 5,60

10 2 5,55
autor: 5,50
0,1 0,2 0,3 0,4 0,5 0,6 0,7
Karolina Sanocka cos q
2
10 1 Rysunek 5 przedstawia wykres zależności
stałej sieciowej od (cos ) dla NaCl.
2
opiekun: 31.116131898, 57.376696906, 83.637261914, 109.897826923, 136.158391931,
Nazywam się Karolina Sanocka i jestem studentką bio- dr Kąt 2θ [°] Eksperymentalna stała sieciowa wyniosła:
a = ( 5,64051 ± 0,00034 ) Å .
fizyki o programie Fizyka Medyczna na Uniwersytecie Paweł Dąbczyńsk Rysunek 2 przedstawia dyfraktogram NaCl bez filtra Podczas eksperymentu wyznaczono również strukturę krystaliczną KCl oraz mieszaninę NaCl i KCl.
niklowego.
4
10
Jagiellońskim. W ostatnich latach studiów staram się

6,45
3
rozwijać swoją wiedzę nie tylko z zakresu biofizyki ale 10 6,40

również w zakresie medycznym. Liczba zliczeń 10 2 6,35

W ramach pracy licencjackiej pod okiem prof. dr hab. a [Å] 6,30

n. med. Ewy Stępień oraz dr inż. Agnieszki Kamińskiej , 10 1 6,25

zajmuję się charakterystyką widm w zakresie średniej 10 0 6,20

podczerwieni uzyskanych dla pęcherzyków zewnątrz- 31.116131898, 57.376696906, 83.637261914, 109.897826923, 136.158391931, 6,15

Kąt 2θ [°] 0,1 0,2 0,3 0,4 0,5 0,6 0,7
komórkowych pochodzących z moczu. Rysunek 3 przedstawia dyfraktogram NaCl z filtrem 2
cos q
niklowym. Rysunek 6 przedstawia wykres zależności
Jestem członkiem Koła Naukowego Biofizyki Mole- Dokonano analizy refleksów dyfraktogramu, określając precyzyjne wartości kątów dla widzialnych pików. Poniższy stałej sieciowej od (cos ) dla KCl.
2
rysunek 3 ukazuje maksimum jednego z pików.
kularnej i Fizyki Medycznej UJ. Eksperymentalna stała sieciowa wyniosła:
a = ( 6,29305 ± 0,00023 ) Å

Moją pasją od dziecka jest malarstwo, brałam udział
Porównano SALVITĘ, która jest mieszaniną NaCl(0,75) i KCl(0,25) z dyfraktogramem NaCl, KCl .
w wielu konkursach, w których osiągałam sukcesy. Poza

malarstwem uwielbiam sport, czytać książki, spacero-

wać oraz grać na gitarze.

Rysunek 4 przedstawia jeden z zaobserwowanych pików

refleksów. Linie ciągłe są dopasowaniami funkcji pseudo-Voigt.

Wyznaczono wskaźniki Millera dla pików posługując się o regułę wygaszeń dla sieci regularnie ściennie centrowanej,
jest to tzw. sieć fcc.

Aby wyznaczyć wskaźniki Millera przyjęto hipotezę, że układ był regularny:

2 2 2
1 (ℎ + + )
= (2)
2 2

ℎ
Z połączenia równania kwadratowego (odległość międzypłaszczyznowa w funkcji wskaźników Millera i parametrów
komórki elementarnej ) oraz równania Bragga (1) otrzymano zmodyfikowane równanie kwadratowe:

2 2 2 2
2 (ℎ + + ) (3)
(sin ) = Rysunek 7 przedstawia porównanie dyfraktogramu NaCl, KCl

4 2
Wartości kątów (sin ) ( = 1,2 … 11) różnią się tylko (h +k +l ). oraz mieszaninę KCl i NaCl.
2
2
2
2

Wartość długości fali jest stała dla każdego z kątów i wynosi λ= 1,54059803 Å, oraz słuszność hipotezy zakłada, że we Podsumowanie i wnioski
wszystkich kierunkach w komórce elementarnej sześciennej jest stałe.
Przy pomocy analizy dyfraktogramu jak i wyznaczeniu wskaźników Millera możliwe było określenie stałej sieci.
Dla każdego z kątów wyliczono następujący iloraz: Eksperymentalna stała sieciowa chlorku sodu wyniosła a=(5,64051 ± 0,00034) Å , natomiast chlorku potasu a=(6,29305 ±

0,00023) Å. Wartości doświadczalne nie są równe w granicach niepewności do wartości referencyjnych, które wynoszą dla
2
sin chlorku sodu a = 5,6405 Å, i chlorku potasu a = 6,2776 Å. Wartości referencyjne stałej sieci znaleziono przy pomocy źródła
= (4)
(sin ) 2 1 [6].
1
Metodą rekurencyjną znaleziono mnożnik, który dla każdego i oddał (h +k +l ) zgodny z regułą wygaszeń sieci fcc co Długość stałej sieciowej zależy m.in. od temperatury. Różnica wynika z tego, iż warunki w czasie dokonywania pomiarów
2
2
2
dowodzi hipotezę. nie były dokładnie takie same jak warunki zawarte w wartościach referencyjnych.
Stosując w równaniu mnożnik, znaleziono takie wartości wskaźników hkl, które naturalnie odtworzyły regułę Rysunek 7 przedstawiający porównanie dyfraktogramu NaCl, KCl oraz mieszaninę

wygaszeń do sieci. W sieci fcc, wskaźniki hkl muszą mieć wartości wszystkie parzyste lub wszystkie nieparzyste. W KCl, ukazuje że dyfraktogram mieszaniny jest sumą dyfraktogramów pomiaru dla NaCl oraz KCl.
sieci fcc, parametr M nie może być równy 1, ponieważ jest wygaszany. Parametr M w takiej sieci ma najmniejszą

wartość równą 3. Bibliografia

Następnie korzystając z Tablicy 2, która znajduje się na stronach 6-8 w źródle [5] przyporządkowano wskaźniki hkl. [1] http://www.2pf.if.uj.edu.pl/

[2] https://pl.wikipedia.org/wiki/Rentgenografia_strukturalna
Aby obliczyć stałą sieciową skorzystano ze wzoru: [3] https://pracownik.kul.pl/files/10722/public/Met_X-ray.pdf

2
2
∗ ℎ + + 2 [4] https://cnx.org/contents/u2KTPvIK@7.4:NKz3qbFO@4/4-6-Dyfrakcja-rentgenowska
= (5)
2∗ [5] http://www.krystalografia.us.edu.pl/mag/mag11.pdf
gdzie, λ długość fali, hkl wskaźniki Millera. [6] http://rruff.geo.arizona.edu/AMS/amcsd.php